Suma y sustracción de vectores.
Podemos sumar vectores de dos maneras: matemáticamente(Analíticamente) o gráficamente.
Sumar vectores de forma gráfica
Consideremos el siguiente problema: una persona se desplaza 8 metros hacia el norte, hasta alcanzar el punto B y, continuando su viaje, se desplaza 6 metros hacia el este, hasta detenerse en el punto C. ¿Cuál ha sido su desplazamiento definitivo o resultante? Su desplazamiento resultante o suma vectorial queda definido por el vector AC, cuyo origen coincide con el vector AB y su extremo con el del vector BC, luego: |  |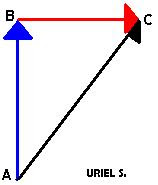
Desplazamiento AB + desplazamiento BC = Vector AC
El anterior es un procedimiento general que se puede aplicar a cualquier par de vectores y su construcción puede resumirse así: para hallar la suma de dos vectores basta desplazar uno de ellos a continuación del otro(El Final del Primero es el inicio del Segundo), el vector suma queda representado por aquel cuyo origen coincide con el del primero y su extremo con el final del segundo. Como lo que en verdad se hace es construir un triángulo, el procedimiento se conoce como método del triángulo.
EJEMPLO 1. RESUELTO POR EL MÉTODO GRÁFICO
Encuentra la suma del vector a con el vector b, es decir; 
, teniendo en cuenta la siguiente figura.
, teniendo en cuenta la siguiente figura.
Solución
Para resolver por el método gráfico la suma de los dos vectores se realiza lo siguiente:
1. Se coloca el vector a
2. Al final del vector a, se coloca el inicio del vector b
3. Luego, para saber cual es la suma del vector a con el vector b. Se pasa una flecha que inicia del principio del vector a hasta el final del vector b, donde encontramos nuestra respuesta de forma gráfica y esta de color rojo.
EJEMPLO 2. RESUELTO POR EL MÉTODO GRÁFICO
Encuentra la suma del vector a con el vector b y el vector c, es decir; también podemos sumar tres (3) vectores al mismo tiempo 
, teniendo en cuenta la ubicación de los vectores libres.
, teniendo en cuenta la ubicación de los vectores libres.
Solución
Para resolver por el método gráfico la suma de los tres vectores, se realiza lo mismo que cuando sumamos dos (2) vectores
1. Se coloca el vector a
2. Al final del vector a, se coloca el inicio del vector b
3. Al final del vector b, se coloca el inicio del vector c
4. para finalizar la suma de los tres (3) vectores. Se traza una flecha que inicia del principio del vector a hasta el final del vector c, donde encontramos nuestra respuesta de forma gráfica y la encontramos de color rojo.
NOTA: para sumar cuatro (4), cinco (5) vectores de la forma gráfica, se realiza de la misma forma presentada anteriormente.
SUMA DE VECTORES DE FORMA ANALITICA
Antes de realizar la suma de vectores por medio de la forma analitica, expliquemos las componentes de un vector
COMPONENTES DE UN VECTOR
Aquí vamos a ver que un vector también puede ser representado por un par de números. Ilustremos en el plano cartesiano los vectores de un sistema de coordenadas. Es decir, un punto origen, y dos ejes perpendiculares. A todo punto P haremos corresponder un par de números que son sus coordenadas (x,y); se escribe P(x,y).
Ejemplo 3
Un vector v queda identificado por los dos siguientes puntos P(2,1) y Q(4,4).Representemos el vector v en un sistema de coordenadas cartesianas, donde tiene origen en P y extremo en Q. ¿Cuáles son las componentes del vector v.
Solución
El vector v queda representado en el plano cartesiano como se ilustra en la siguiente figura.
Para encontrar las componentes del vector v, procedemos como se muestra más adelante.
 | el vector v es igual al vector PQ |
 = (XQ - Xp , YQ - Yp) | El vector v es igual a la resta de las componentes de los punto P y Q. |
| = (4 - 2 , 4 - 1) | El vector v es igual a la resta de las componentes numérica de los punto P(2,1) y Q(4,4). |
| = ( 2 , 3 ) | El vector v es igual a las componentes numérica ( 2 , 3). |
NOTA:
- No hay que confundir las componentes del vector con las coordenadas de un punto, el contexto en el que nos estemos manejando nos aclarará dicha situación.
- No es lo mismo decir que estamos en el punto (2,3) a que nos movimos 2 pasos a la derecha del eje horizontal y luego 3 pasos hacia arriba del eje vertical.
Ejercicio 1
Dados los seis vectores
calcula:
- Las componentes del vector AB
- Las coordenadas del punto D
- Las coordenadas del punto E
- Las componentes del vector GH
- Las coordenadas del punto I
- Las coordenadas del punto M
ACTIVIDAD 1
Regla del triángulo para sumar vectores. Componentes expresadas como (x, y). Observación: Saca un vector del tarro y comienza a mirar y/o observar
. Cuando coloques el vector en el plano cartesiano, al doble click sobre el vector y detalla los valores que aparecen en el cuadro que mencionamos anteriormente. Puedes sacar la cantidad de vectores o flechas que desees para tu aprendizaje. Ensaya los demás botones del simulador. ¿Puedes deducir en qué consiste la regla del triángulo?
Autor: PhET Pag. Web: La adición de vectores |
ACTIVIDAD 2
Con esta actividad se busca ampliar los aprendizajes adquiridos en clase.
En esta actividad debes buscar en sitio web: Educaplus y posteriormente colocar en su buscador la palabra vectores. Encontraras varios simuladores, en los cuales debes analizar sus funciones y que utilidades tienen para nuestro aprendizaje
En esta actividad debes buscar en sitio web: Educaplus y posteriormente colocar en su buscador la palabra vectores. Encontraras varios simuladores, en los cuales debes analizar sus funciones y que utilidades tienen para nuestro aprendizaje
 |  |  |
| Elementos de un Vector |